■これまでのおはなし
■<理論>教えてもらった計算のコツ
①並列接続の2抵抗の計算方法
抵抗R1、R2が並列に接続されている場合の、合成抵抗Rの求め方は、次の通りです。
R=R1*R2/(R1+R2)・・・(1)
「和分の積」と覚えられていると思います。
これだけでも難しくはないのですが、この(1)式をさらに変形します。
分子分母をR1で割ると、
R={(R1*R2)/R1}/{(R1+R2)/R1}=R2/{1+(R2/R1)}
となります。
※ただしR1<R2
つまり、大きいほうの抵抗値R2は、小さいほうの抵抗値R1の何倍か。
それに+1をして、R2を割ることで、合成抵抗が求められます。
これ実際にやってみるとわかるのですが、このコツのやり方の方が早いです。
計算らしい計算せずとも正しく求められます。
だいたいR1とR2は互いに割り切れる数で出題されることが多いので、分子のR2の数字を書いてる時点で、分母のところは暗算で一瞬で出せています。
私も実際の試験では使いました。
けっこうおすすめです。
②キルヒホッフ第二法則の代わりにミルマンの定理を使う
キルヒホッフの第二法則といえば、閉回路作って電圧の方程式を解いていかなければいけないめんどくさい手法です。
正直、時間が足りない試験ではやってられないです。
そんなときこそミルマンの定理です。
これは、電源の並列回路の端子電圧を求める定理です。
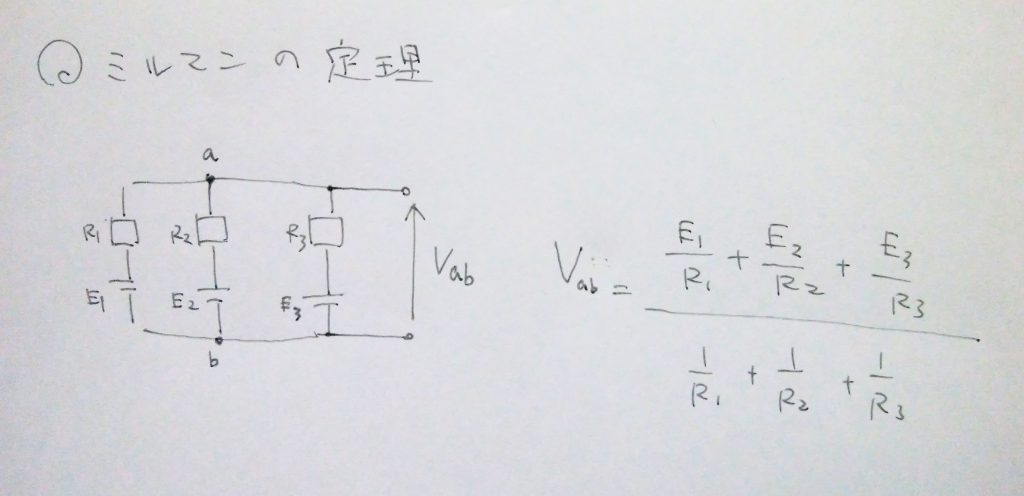
試験では似たような回路図の、電圧やら電流やら求める問題が多いのですが、、、
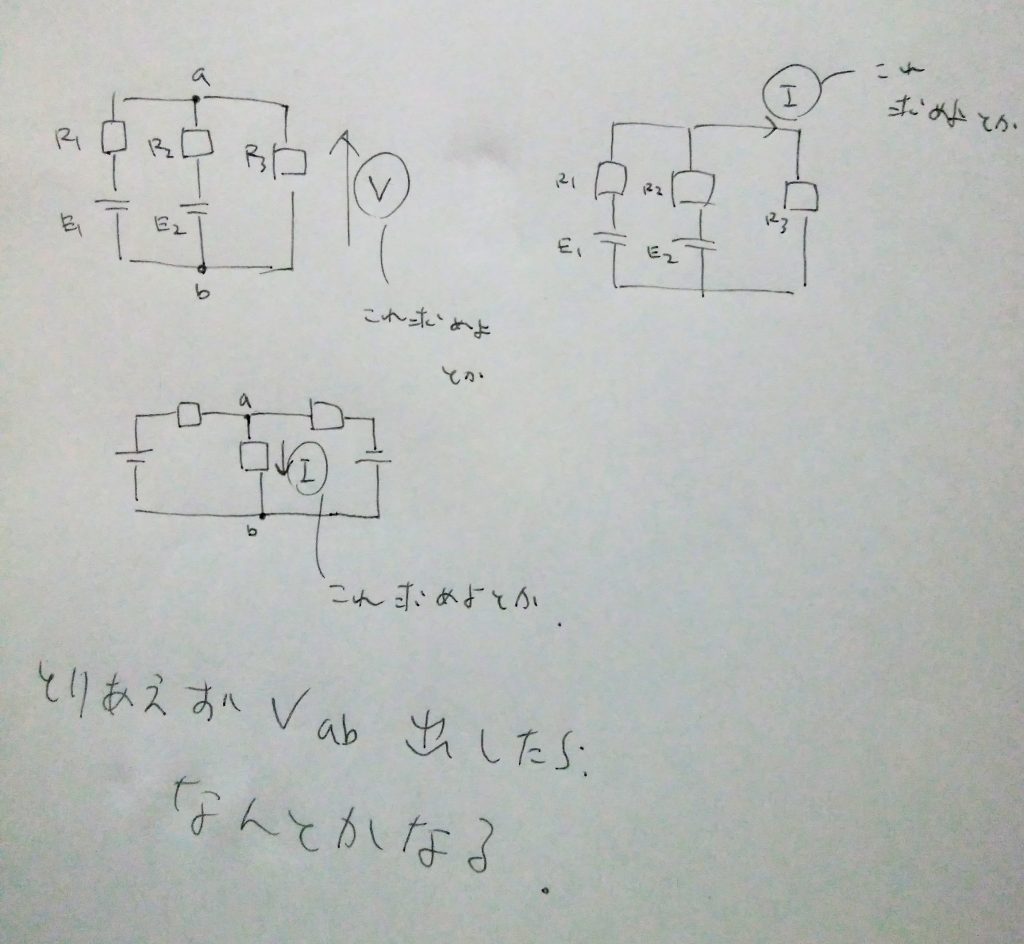
とりあえず最初にミルマンの定理でさくっとVab出したら、あとはなんとかなります。
このやり方は、かなり重宝しました。
参考:
http://eleking.net/k21/k21t/k21t-kirchhoff.html
http://denken3.sakuraweb.com/topics/electricity/millmans_theorem/10.shtml
※とはいえ、理解しきれていない定理とかだったら、焦るとわけわかんなくなることもあります。
そんなときは、確実にできるキルヒホッフの第二法則とか基本的なところに立ち返って、落ち着いて問題に取り組むことをおすすめします。
→【電験三種】合格体験記 その8へ
※2020/6/2 プラグイン不具合のため数式表示がおかしかったところを書き直しました。







